import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from pandas.plotting import register_matplotlib_converters
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.stattools import acf, pacf
from statsmodels.tsa.arima.model import ARIMA
from datetime import datetime, timedelta
register_matplotlib_converters()
5: Generate Some Data#
\(y_t = 50 + 0.4\varepsilon_{t-1} + 0.3\varepsilon_{t-2} + \varepsilon_t\)#
\(\varepsilon_t \sim N(0,1)\)#
errors = np.random.normal(0, 1, 400)
date_index = pd.date_range(start='9/1/2019', end='1/1/2020')
mu = 50
series = []
for t in range(1,len(date_index)+1):
series.append(mu + 0.4*errors[t-1] + 0.3*errors[t-2] + errors[t])
series = pd.Series(series, date_index)
series = series.asfreq(pd.infer_freq(series.index))
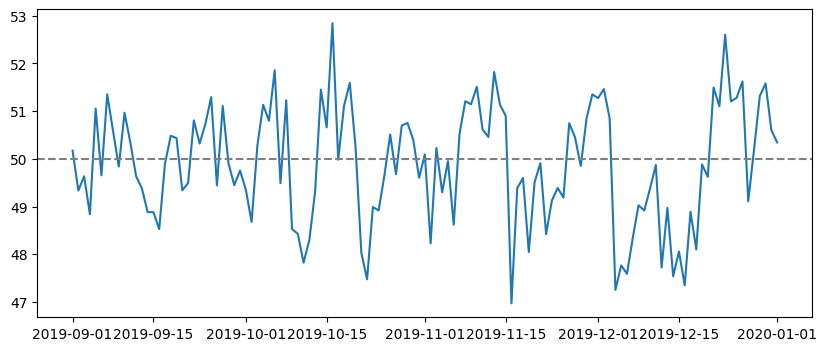
plt.figure(figsize=(10,4))
plt.plot(series)
plt.axhline(mu, linestyle='--', color='grey')
<matplotlib.lines.Line2D at 0x7f420c12d400>
def calc_corr(series, lag):
return pearsonr(series[:-lag], series[lag:])[0]
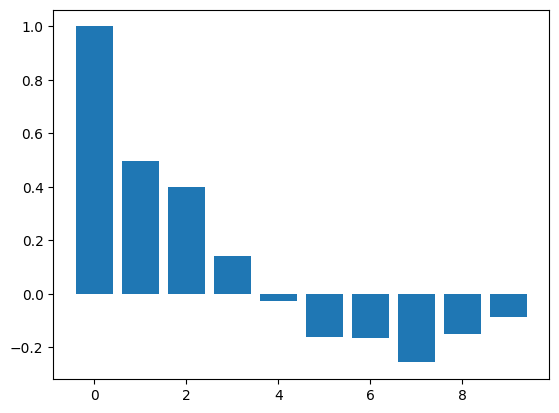
ACF#
acf_vals = acf(series)
num_lags = 10
plt.bar(range(num_lags), acf_vals[:num_lags])
<BarContainer object of 10 artists>
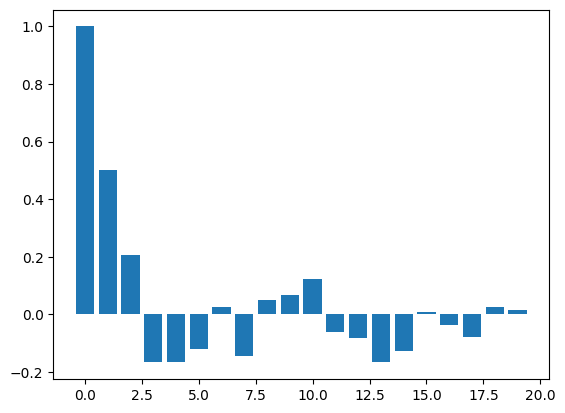
PACF#
pacf_vals = pacf(series)
num_lags = 20
plt.bar(range(num_lags), pacf_vals[:num_lags])
<BarContainer object of 20 artists>
Get training and testing sets#
train_end = datetime(2019,12,30)
test_end = datetime(2020,1,1)
train_data = series[:train_end]
test_data = series[train_end + timedelta(days=1):test_end]
Fit ARIMA Model#
ARIMA?
#create the model
model = ARIMA(train_data, order=(0,0,2))
#fit the model
model_fit = model.fit()
#summary of the model
print(model_fit.summary())
SARIMAX Results
==============================================================================
Dep. Variable: y No. Observations: 121
Model: ARIMA(0, 0, 2) Log Likelihood -177.787
Date: Wed, 22 Mar 2023 AIC 363.575
Time: 12:58:21 BIC 374.758
Sample: 09-01-2019 HQIC 368.117
- 12-30-2019
Covariance Type: opg
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 49.8920 0.171 292.359 0.000 49.557 50.226
ma.L1 0.3305 0.094 3.498 0.000 0.145 0.516
ma.L2 0.3725 0.088 4.220 0.000 0.199 0.546
sigma2 1.1027 0.143 7.704 0.000 0.822 1.383
===================================================================================
Ljung-Box (L1) (Q): 0.94 Jarque-Bera (JB): 4.17
Prob(Q): 0.33 Prob(JB): 0.12
Heteroskedasticity (H): 1.77 Skew: -0.44
Prob(H) (two-sided): 0.08 Kurtosis: 3.20
===================================================================================
Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
Predicted Model:#
\(\hat{y}_t = 50 + 0.37\varepsilon_{t-1} + 0.25\varepsilon_{t-2}\)#
#get prediction start and end dates
pred_start_date = test_data.index[0]
pred_end_date = test_data.index[-1]
#get the predictions and residuals
predictions = model_fit.predict(start=pred_start_date, end=pred_end_date)
residuals = test_data - predictions
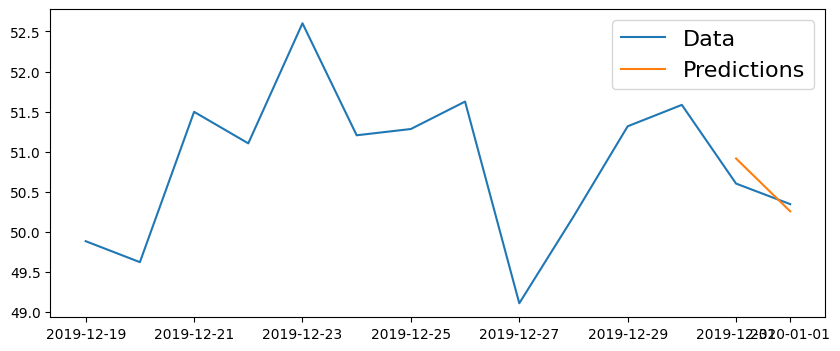
plt.figure(figsize=(10,4))
plt.plot(series[-14:])
plt.plot(predictions)
plt.legend(('Data', 'Predictions'), fontsize=16)
<matplotlib.legend.Legend at 0x7f4205f2c580>
print('Mean Absolute Percent Error:', round(np.mean(abs(residuals/test_data)),4))
Mean Absolute Percent Error: 0.004
print('Root Mean Squared Error:', np.sqrt(np.mean(residuals**2)))
Root Mean Squared Error: 0.23016330452025244

