Ctrl+K

7: Model Selection

import pandas as pd
from datetime import datetime
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.arima.model import ARIMA
from statsmodels.tsa.stattools import adfuller

7: Model Selection#

def parser(s):
    return datetime.strptime(s, '%Y-%m-%d')

def perform_adf_test(series):
    result = adfuller(series)
    print('ADF Statistic: %f' % result[0])
    print('p-value: %f' % result[1])

#get data
series = pd.read_csv('../data/catfish.csv', parse_dates=[0], index_col=0)
series = series.asfreq(pd.infer_freq(series.index))
series = series.loc[datetime(2004,1,1):]
series = series.diff().diff().dropna()

#check stationarity
perform_adf_test(series)

ADF Statistic: -7.162321
p-value: 0.000000

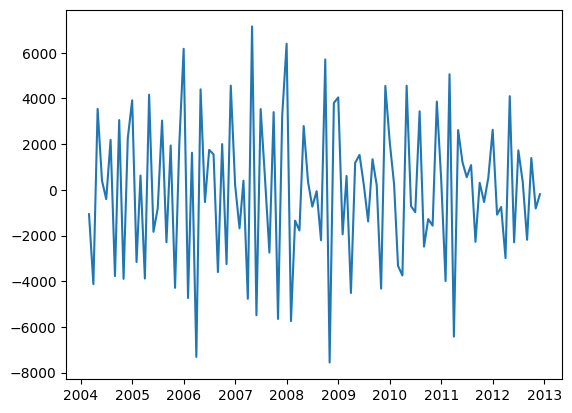
plt.plot(series)

[<matplotlib.lines.Line2D at 0x7f4d9ffaa9d0>]
../../../_images/29b94e030c303edcb2b26b2638983e3e9e8d6d80e20bd121465088558d31f8e7.png 
plot_pacf(series, lags=10)
plt.show()

/home/ubuntu/Documents/Projects/STI_FX_Intervention/.venv/lib/python3.9/site-packages/statsmodels/graphics/tsaplots.py:348: FutureWarning: The default method 'yw' can produce PACF values outside of the [-1,1] interval. After 0.13, the default will change tounadjusted Yule-Walker ('ywm'). You can use this method now by setting method='ywm'.
  warnings.warn(
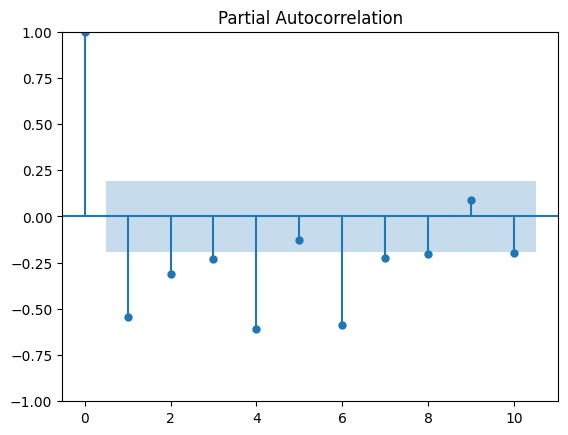
../../../_images/fdf5857f1417a82fed697c32ab6995ee23f33eeb3b51072e5a1753fa6517d061.png

Either AR(1), AR(4), AR(6), or AR(10)#

plt.figure(figsize=(12,12))

ar_orders = [1, 4, 6, 10]
fitted_model_dict = {}

for idx, ar_order in enumerate(ar_orders):
    
    #create AR(p) model
    ar_model = ARIMA(series, order=(ar_order,0,0))
    ar_model_fit = ar_model.fit()
    fitted_model_dict[ar_order] = ar_model_fit
    plt.subplot(4,1,idx+1)
    plt.plot(series)
    plt.plot(ar_model_fit.fittedvalues)
    plt.title('AR(%s) Fit'%ar_order, fontsize=16)

plt.tight_layout()
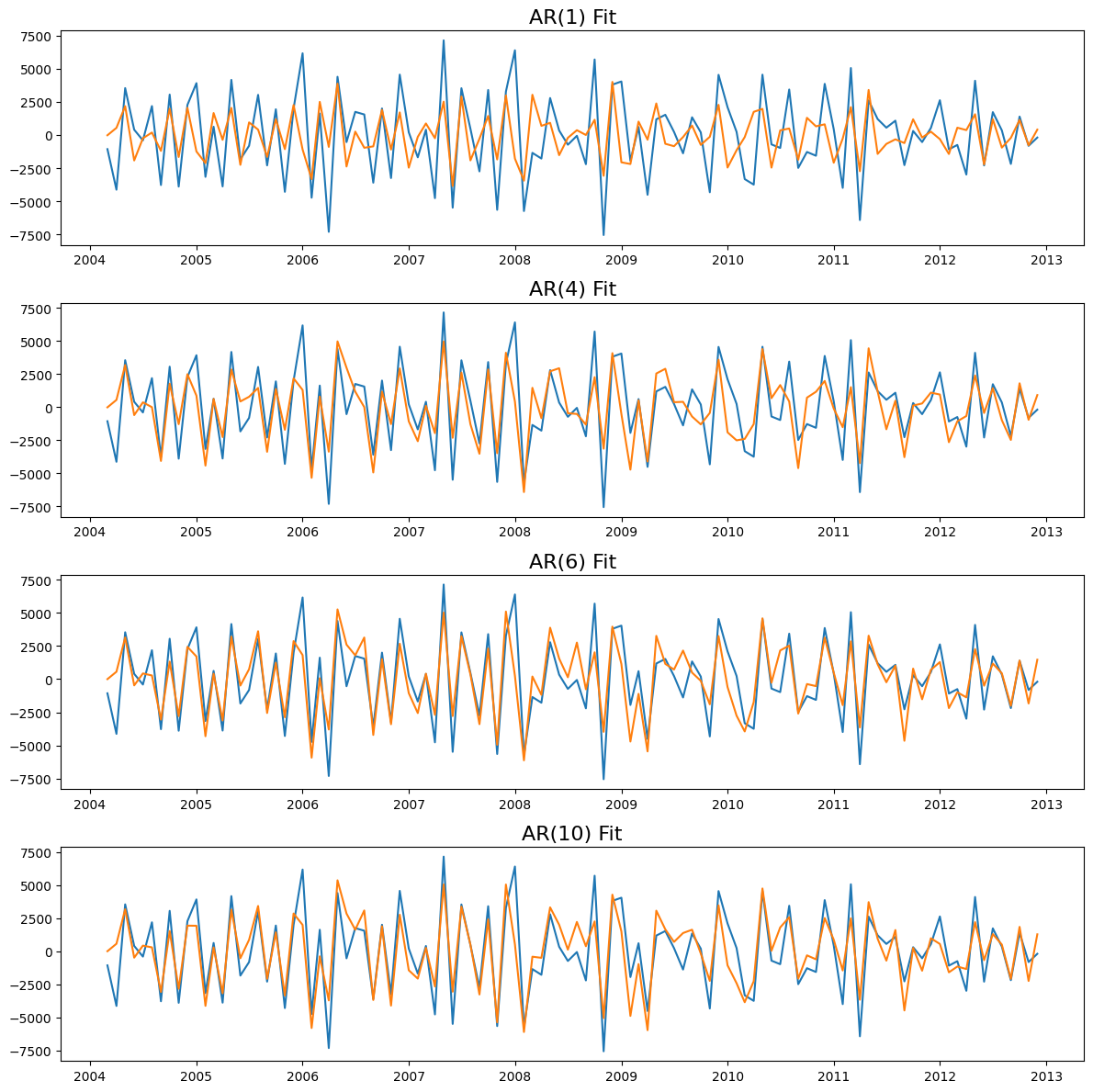
../../../_images/cfbecb9971f8857571e68a7b24723cb0c77dac2b70ad54a24721e6178243ffc2.png

Model Selection#

Each model has:

  • a log likelihood (\(l\))

  • a number of parameters (\(k\))

  • a number of samples used for fitting (\(n\))

\(AIC = 2k - 2l\)

Lower AIC via higher log likelihood or less parameters

\(BIC = \)\ln(n)k - 2l$

Lower BIC via higher log likelihood or less parameters or less samples used in fitting

#AIC comparison
for ar_order in ar_orders:
    print('AIC for AR(%s): %s'%(ar_order, fitted_model_dict[ar_order].aic))

AIC for AR(1): 1980.860621744531
AIC for AR(4): 1927.6099852660486
AIC for AR(6): 1899.6497442306497
AIC for AR(10): 1902.376544968234

Based on AIC criteria, pick AR(6)#

#BIC comparison
for ar_order in ar_orders:
    print('BIC for AR(%s): %s'%(ar_order, fitted_model_dict[ar_order].bic))

BIC for AR(1): 1988.8509390268673
BIC for AR(4): 1943.590619830721
BIC for AR(6): 1920.9572569835464
BIC for AR(10): 1934.3378140975788

Based on BIC criteria, pick AR(6)#

Contents