import pandas as pd
from datetime import datetime
import matplotlib.pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
from statsmodels.tsa.api import VAR
from scipy.stats import pearsonr
13: VAR Model#
def parser(s):
return datetime.strptime(s, '%Y-%m')
ice_cream_heater_df = pd.read_csv('../data/ice_cream_vs_heater.csv', parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
/tmp/ipykernel_3777724/10753663.py:1: FutureWarning: The squeeze argument has been deprecated and will be removed in a future version. Append .squeeze("columns") to the call to squeeze.
ice_cream_heater_df = pd.read_csv('../data/ice_cream_vs_heater.csv', parse_dates=[0], index_col=0, squeeze=True, date_parser=parser)
ice_cream_heater_df = ice_cream_heater_df.asfreq(pd.infer_freq(ice_cream_heater_df.index))
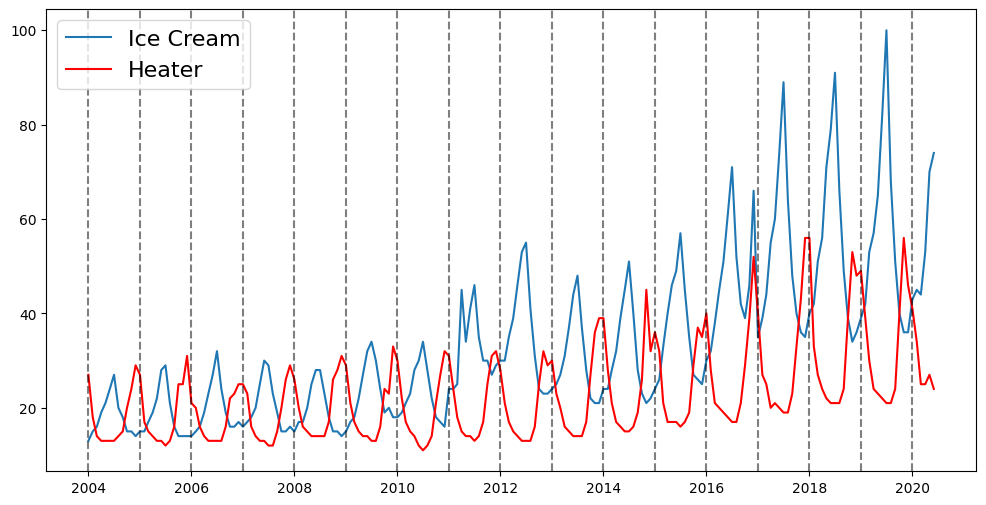
plt.figure(figsize=(12,6))
ice_cream, = plt.plot(ice_cream_heater_df['ice cream'])
heater, = plt.plot(ice_cream_heater_df['heater'], color='red')
for year in range(2004, 2021):
plt.axvline(datetime(year,1,1), linestyle='--', color='k', alpha=0.5)
plt.legend(['Ice Cream', 'Heater'], fontsize=16)
<matplotlib.legend.Legend at 0x7f12641759d0>
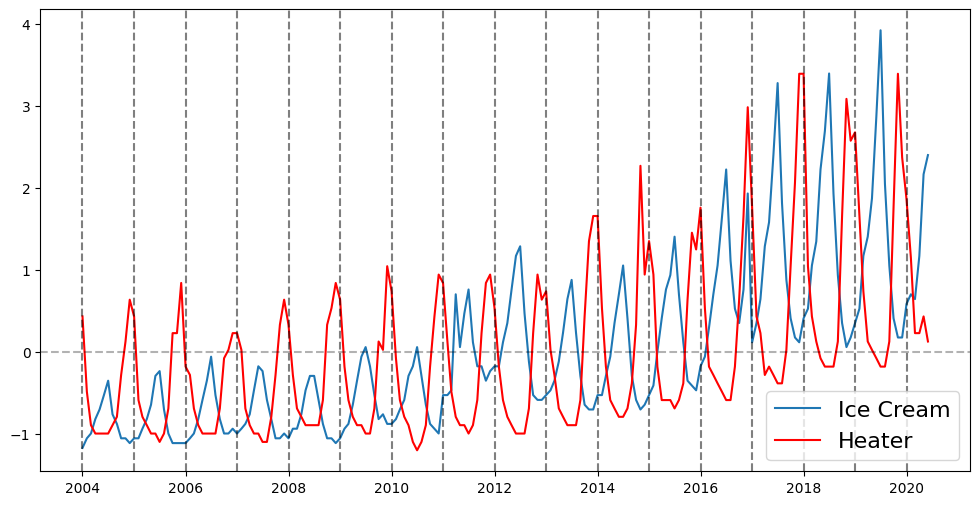
Normalize#
avgs = ice_cream_heater_df.mean()
devs = ice_cream_heater_df.std()
for col in ice_cream_heater_df.columns:
ice_cream_heater_df[col] = (ice_cream_heater_df[col] - avgs.loc[col]) / devs.loc[col]
plt.figure(figsize=(12,6))
ice_cream, = plt.plot(ice_cream_heater_df['ice cream'])
heater, = plt.plot(ice_cream_heater_df['heater'], color='red')
for year in range(2004, 2021):
plt.axvline(datetime(year,1,1), linestyle='--', color='k', alpha=0.5)
plt.axhline(0, linestyle='--', color='k', alpha=0.3)
plt.legend(['Ice Cream', 'Heater'], fontsize=16)
<matplotlib.legend.Legend at 0x7f12620bbbe0>
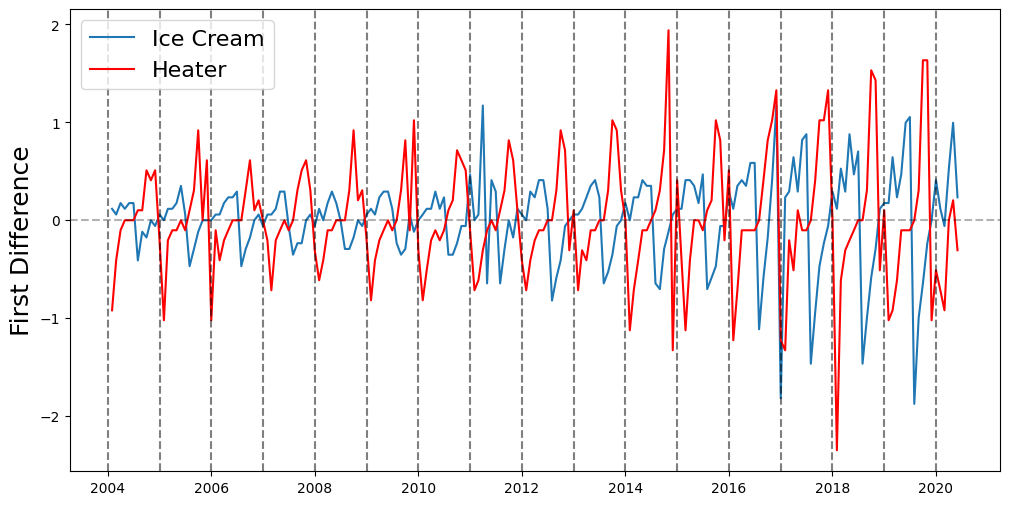
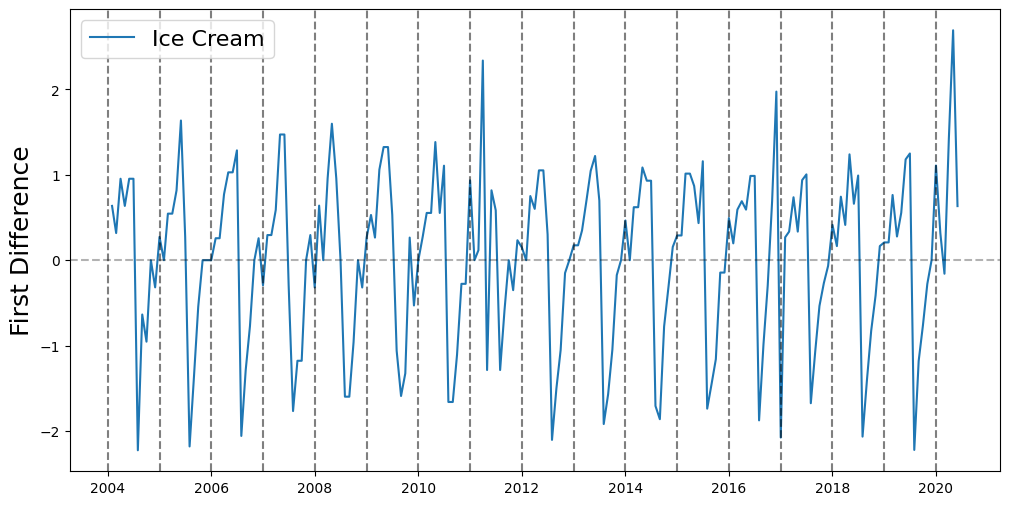
Take First Difference to Remove Trend#
ice_cream_heater_df = ice_cream_heater_df.diff().dropna()
plt.figure(figsize=(12,6))
ice_cream, = plt.plot(ice_cream_heater_df['ice cream'])
heater, = plt.plot(ice_cream_heater_df['heater'], color='red')
for year in range(2004, 2021):
plt.axvline(datetime(year,1,1), linestyle='--', color='k', alpha=0.5)
plt.axhline(0, linestyle='--', color='k', alpha=0.3)
plt.ylabel('First Difference', fontsize=18)
plt.legend(['Ice Cream', 'Heater'], fontsize=16)
<matplotlib.legend.Legend at 0x7f1261fc3f10>
plt.figure(figsize=(12,6))
ice_cream, = plt.plot(ice_cream_heater_df['ice cream'])
for year in range(2004, 2021):
plt.axvline(datetime(year,1,1), linestyle='--', color='k', alpha=0.5)
plt.axhline(0, linestyle='--', color='k', alpha=0.3)
plt.ylabel('First Difference', fontsize=18)
plt.legend(['Ice Cream'], fontsize=16)
<matplotlib.legend.Legend at 0x7f1261f15520>
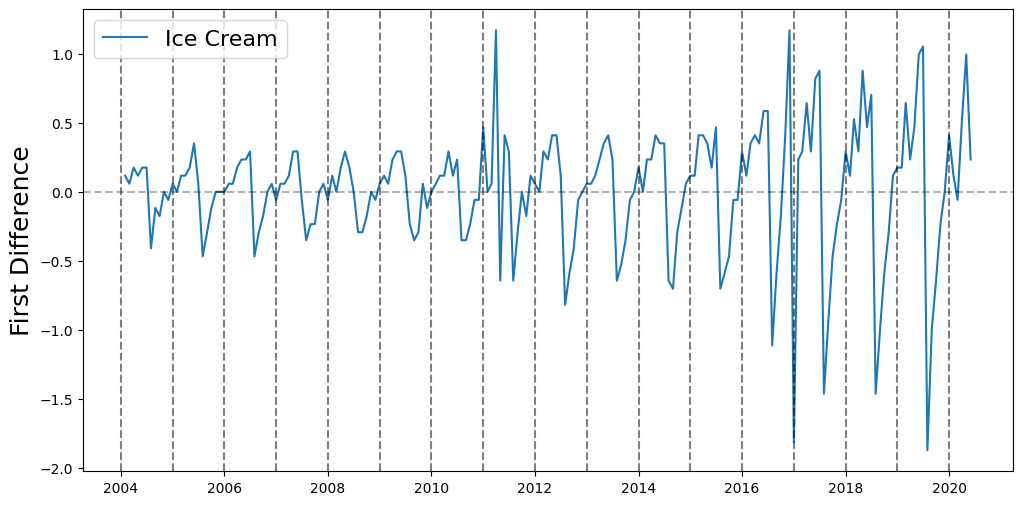
Remove Increasing Volatility#
annual_volatility = ice_cream_heater_df.groupby(ice_cream_heater_df.index.year).std()
annual_volatility
| heater | ice cream | |
|---|---|---|
| Month | ||
| 2004 | 0.415481 | 0.184201 |
| 2005 | 0.474527 | 0.214837 |
| 2006 | 0.400148 | 0.227698 |
| 2007 | 0.359839 | 0.198947 |
| 2008 | 0.396182 | 0.183239 |
| 2009 | 0.499810 | 0.221038 |
| 2010 | 0.459566 | 0.211668 |
| 2011 | 0.443924 | 0.501018 |
| 2012 | 0.471104 | 0.389711 |
| 2013 | 0.503587 | 0.335840 |
| 2014 | 0.855743 | 0.377482 |
| 2015 | 0.569441 | 0.404340 |
| 2016 | 0.719843 | 0.593347 |
| 2017 | 0.830886 | 0.874263 |
| 2018 | 0.987221 | 0.708785 |
| 2019 | 0.892991 | 0.843598 |
| 2020 | 0.426657 | 0.369810 |
ice_cream_heater_df['ice_cream_annual_vol'] = ice_cream_heater_df.index.map(lambda d: annual_volatility.loc[d.year, 'ice cream'])
ice_cream_heater_df['heater_annual_vol'] = ice_cream_heater_df.index.map(lambda d: annual_volatility.loc[d.year, 'heater'])
ice_cream_heater_df
| heater | ice cream | ice_cream_annual_vol | heater_annual_vol | |
|---|---|---|---|---|
| Month | ||||
| 2004-02-01 | -0.918789 | 0.117140 | 0.184201 | 0.415481 |
| 2004-03-01 | -0.408351 | 0.058570 | 0.184201 | 0.415481 |
| 2004-04-01 | -0.102088 | 0.175710 | 0.184201 | 0.415481 |
| 2004-05-01 | 0.000000 | 0.117140 | 0.184201 | 0.415481 |
| 2004-06-01 | 0.000000 | 0.175710 | 0.184201 | 0.415481 |
| ... | ... | ... | ... | ... |
| 2020-02-01 | -0.714614 | 0.117140 | 0.369810 | 0.426657 |
| 2020-03-01 | -0.918789 | -0.058570 | 0.369810 | 0.426657 |
| 2020-04-01 | 0.000000 | 0.527129 | 0.369810 | 0.426657 |
| 2020-05-01 | 0.204175 | 0.995687 | 0.369810 | 0.426657 |
| 2020-06-01 | -0.306263 | 0.234279 | 0.369810 | 0.426657 |
197 rows × 4 columns
ice_cream_heater_df['ice cream'] = ice_cream_heater_df['ice cream'] / ice_cream_heater_df['ice_cream_annual_vol']
ice_cream_heater_df['heater'] = ice_cream_heater_df['heater'] / ice_cream_heater_df['heater_annual_vol']
plt.figure(figsize=(12,6))
ice_cream, = plt.plot(ice_cream_heater_df['ice cream'])
for year in range(2004, 2021):
plt.axvline(datetime(year,1,1), linestyle='--', color='k', alpha=0.5)
plt.axhline(0, linestyle='--', color='k', alpha=0.3)
plt.ylabel('First Difference', fontsize=18)
plt.legend(['Ice Cream'], fontsize=16)
<matplotlib.legend.Legend at 0x7f1261bb7a00>
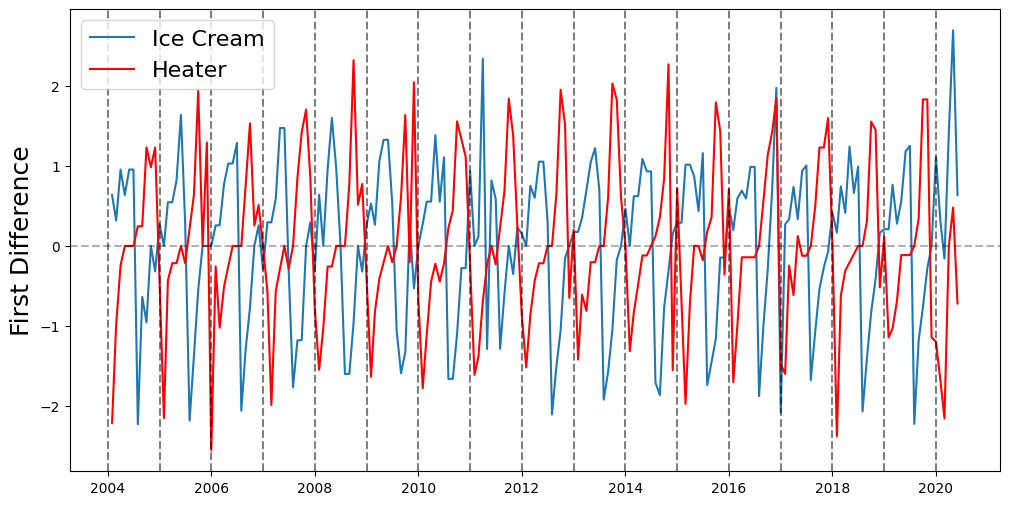
plt.figure(figsize=(12,6))
ice_cream, = plt.plot(ice_cream_heater_df['ice cream'])
heater, = plt.plot(ice_cream_heater_df['heater'], color='red')
for year in range(2004, 2021):
plt.axvline(datetime(year,1,1), linestyle='--', color='k', alpha=0.5)
plt.axhline(0, linestyle='--', color='k', alpha=0.3)
plt.ylabel('First Difference', fontsize=18)
plt.legend(['Ice Cream', 'Heater'], fontsize=16)
<matplotlib.legend.Legend at 0x7f1261af2af0>
Remove Seasonality#
month_avgs = ice_cream_heater_df.groupby(ice_cream_heater_df.index.month).mean()
print(month_avgs)
heater ice cream ice_cream_annual_vol heater_annual_vol
Month
1 -0.428360 0.130345 0.415976 0.580717
2 -1.483129 0.250194 0.402342 0.570997
3 -1.063595 0.433016 0.402342 0.570997
4 -0.442926 0.838085 0.402342 0.570997
5 -0.121663 0.967273 0.402342 0.570997
6 -0.128425 0.987311 0.402342 0.570997
7 -0.107093 0.735052 0.404376 0.580018
8 0.075720 -1.821285 0.404376 0.580018
9 0.544638 -1.307661 0.404376 0.580018
10 1.613170 -0.830889 0.404376 0.580018
11 1.183118 -0.088136 0.404376 0.580018
12 0.491641 0.088998 0.404376 0.580018
ice_cream_heater_df['ice_cream_month_avg'] = ice_cream_heater_df.index.map(lambda d: month_avgs.loc[d.month, 'ice cream'])
ice_cream_heater_df['heater_month_avg'] = ice_cream_heater_df.index.map(lambda d: month_avgs.loc[d.month, 'heater'])
ice_cream_heater_df
| heater | ice cream | ice_cream_annual_vol | heater_annual_vol | ice_cream_month_avg | heater_month_avg | |
|---|---|---|---|---|---|---|
| Month | ||||||
| 2004-02-01 | -2.211387 | 0.635934 | 0.184201 | 0.415481 | 0.250194 | -1.483129 |
| 2004-03-01 | -0.982838 | 0.317967 | 0.184201 | 0.415481 | 0.433016 | -1.063595 |
| 2004-04-01 | -0.245710 | 0.953901 | 0.184201 | 0.415481 | 0.838085 | -0.442926 |
| 2004-05-01 | 0.000000 | 0.635934 | 0.184201 | 0.415481 | 0.967273 | -0.121663 |
| 2004-06-01 | 0.000000 | 0.953901 | 0.184201 | 0.415481 | 0.987311 | -0.128425 |
| ... | ... | ... | ... | ... | ... | ... |
| 2020-02-01 | -1.674916 | 0.316756 | 0.369810 | 0.426657 | 0.250194 | -1.483129 |
| 2020-03-01 | -2.153463 | -0.158378 | 0.369810 | 0.426657 | 0.433016 | -1.063595 |
| 2020-04-01 | 0.000000 | 1.425403 | 0.369810 | 0.426657 | 0.838085 | -0.442926 |
| 2020-05-01 | 0.478547 | 2.692427 | 0.369810 | 0.426657 | 0.967273 | -0.121663 |
| 2020-06-01 | -0.717821 | 0.633512 | 0.369810 | 0.426657 | 0.987311 | -0.128425 |
197 rows × 6 columns
ice_cream_heater_df['ice cream'] = ice_cream_heater_df['ice cream'] - ice_cream_heater_df['ice_cream_month_avg']
ice_cream_heater_df['heater'] = ice_cream_heater_df['heater'] - ice_cream_heater_df['heater_month_avg']
ice_cream_heater_df
| heater | ice cream | ice_cream_annual_vol | heater_annual_vol | ice_cream_month_avg | heater_month_avg | |
|---|---|---|---|---|---|---|
| Month | ||||||
| 2004-02-01 | -0.728257 | 0.385740 | 0.184201 | 0.415481 | 0.250194 | -1.483129 |
| 2004-03-01 | 0.080757 | -0.115049 | 0.184201 | 0.415481 | 0.433016 | -1.063595 |
| 2004-04-01 | 0.197217 | 0.115816 | 0.184201 | 0.415481 | 0.838085 | -0.442926 |
| 2004-05-01 | 0.121663 | -0.331339 | 0.184201 | 0.415481 | 0.967273 | -0.121663 |
| 2004-06-01 | 0.128425 | -0.033411 | 0.184201 | 0.415481 | 0.987311 | -0.128425 |
| ... | ... | ... | ... | ... | ... | ... |
| 2020-02-01 | -0.191787 | 0.066562 | 0.369810 | 0.426657 | 0.250194 | -1.483129 |
| 2020-03-01 | -1.089868 | -0.591394 | 0.369810 | 0.426657 | 0.433016 | -1.063595 |
| 2020-04-01 | 0.442926 | 0.587318 | 0.369810 | 0.426657 | 0.838085 | -0.442926 |
| 2020-05-01 | 0.600210 | 1.725154 | 0.369810 | 0.426657 | 0.967273 | -0.121663 |
| 2020-06-01 | -0.589396 | -0.353799 | 0.369810 | 0.426657 | 0.987311 | -0.128425 |
197 rows × 6 columns
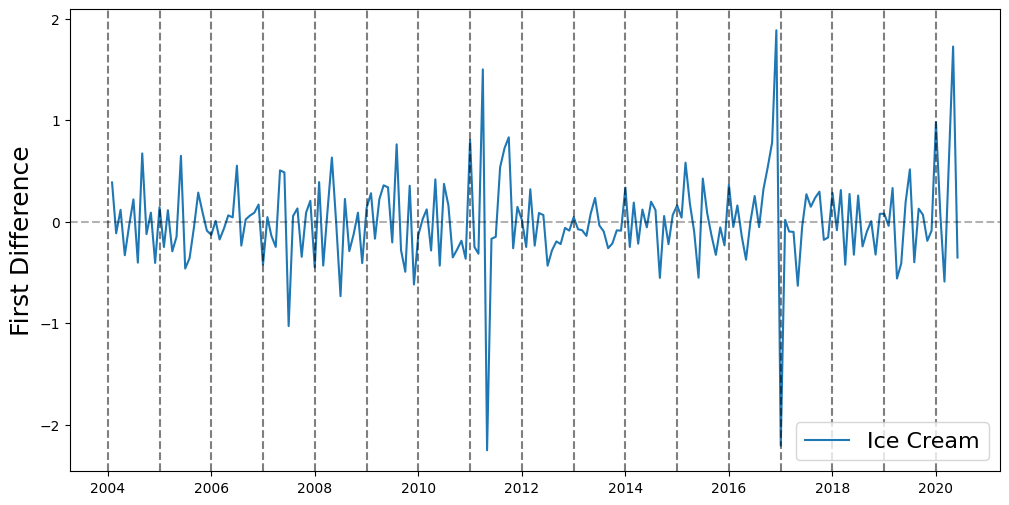
plt.figure(figsize=(12,6))
ice_cream, = plt.plot(ice_cream_heater_df['ice cream'])
for year in range(2004, 2021):
plt.axvline(datetime(year,1,1), linestyle='--', color='k', alpha=0.5)
plt.axhline(0, linestyle='--', color='k', alpha=0.3)
plt.ylabel('First Difference', fontsize=18)
plt.legend(['Ice Cream'], fontsize=16)
<matplotlib.legend.Legend at 0x7f1260157fd0>
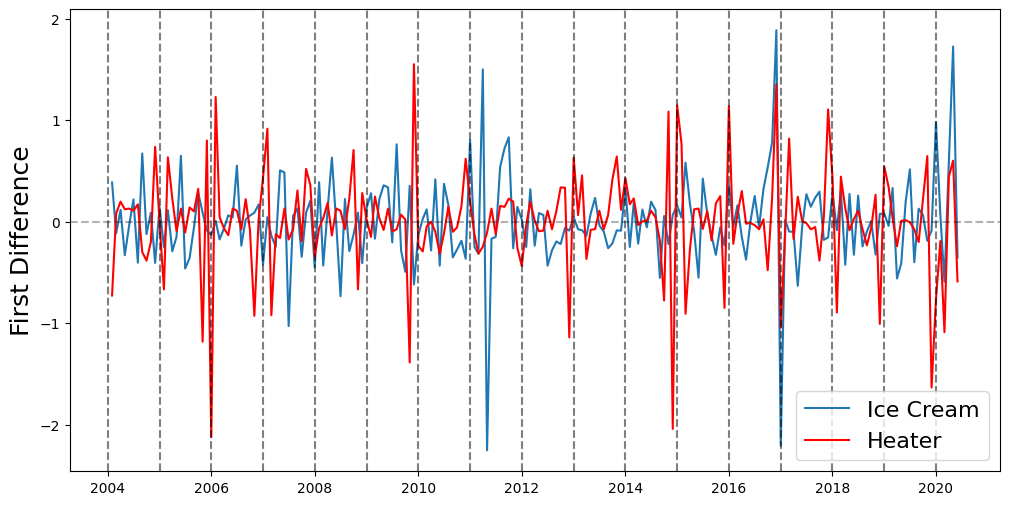
plt.figure(figsize=(12,6))
ice_cream, = plt.plot(ice_cream_heater_df['ice cream'])
heater, = plt.plot(ice_cream_heater_df['heater'], color='red')
for year in range(2004, 2021):
plt.axvline(datetime(year,1,1), linestyle='--', color='k', alpha=0.5)
plt.axhline(0, linestyle='--', color='k', alpha=0.3)
plt.ylabel('First Difference', fontsize=18)
plt.legend(['Ice Cream', 'Heater'], fontsize=16)
<matplotlib.legend.Legend at 0x7f126009e610>
PACF - Heater#
plot_pacf(ice_cream_heater_df['heater'])
plt.show()
/home/ubuntu/Documents/Projects/STI_FX_Intervention/.venv/lib/python3.9/site-packages/statsmodels/graphics/tsaplots.py:348: FutureWarning: The default method 'yw' can produce PACF values outside of the [-1,1] interval. After 0.13, the default will change tounadjusted Yule-Walker ('ywm'). You can use this method now by setting method='ywm'.
warnings.warn(
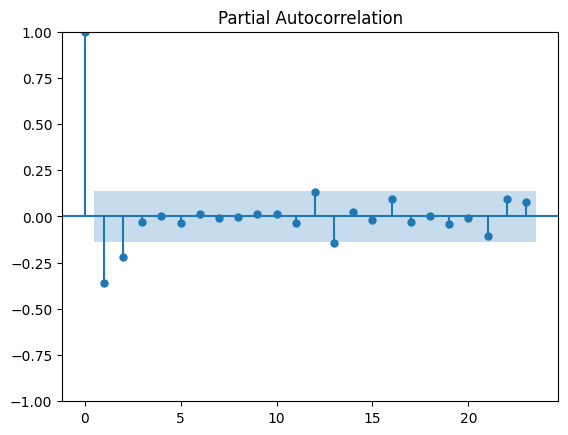
So consider an AR(2)#
Correlation between “heater” and lagged “ice cream”#
for lag in range(1, 14):
heater_series = ice_cream_heater_df['heater'].iloc[lag:]
lagged_ice_cream_series = ice_cream_heater_df['ice cream'].iloc[:-lag]
print('Lag: %s'%lag)
print(pearsonr(heater_series, lagged_ice_cream_series))
print('------')
Lag: 1
PearsonRResult(statistic=-0.031544507425915636, pvalue=0.6607284991749385)
------
Lag: 2
PearsonRResult(statistic=-0.09872703210944635, pvalue=0.16970841905089779)
------
Lag: 3
PearsonRResult(statistic=-0.0017838553789235895, pvalue=0.9803056762960977)
------
Lag: 4
PearsonRResult(statistic=0.060239718598255415, pvalue=0.40529798325286276)
------
Lag: 5
PearsonRResult(statistic=-0.054034864480150276, pvalue=0.45664426275056963)
------
Lag: 6
PearsonRResult(statistic=0.06461183026553836, pvalue=0.3745300043445426)
------
Lag: 7
PearsonRResult(statistic=-0.04949334618415865, pvalue=0.49768766857620883)
------
Lag: 8
PearsonRResult(statistic=0.07890837135977341, pvalue=0.28045489704330623)
------
Lag: 9
PearsonRResult(statistic=-0.0532350169960043, pvalue=0.4681034202228026)
------
Lag: 10
PearsonRResult(statistic=0.029536989060791177, pvalue=0.6882054906333271)
------
Lag: 11
PearsonRResult(statistic=-0.059795363515225686, pvalue=0.41752174204856846)
------
Lag: 12
PearsonRResult(statistic=-0.07513046035981792, pvalue=0.3094409252542678)
------
Lag: 13
PearsonRResult(statistic=0.19808902198429754, pvalue=0.007029107082073456)
------
Fit a VAR Model#
ice_cream_heater_df = ice_cream_heater_df[['ice cream', 'heater']]
model = VAR(ice_cream_heater_df)
model_fit = model.fit(maxlags=13)
model_fit.summary()
Summary of Regression Results
==================================
Model: VAR
Method: OLS
Date: Wed, 22, Mar, 2023
Time: 13:23:17
--------------------------------------------------------------------
No. of Equations: 2.00000 BIC: -1.92349
Nobs: 184.000 HQIC: -2.48459
Log likelihood: -204.405 FPE: 0.0571123
AIC: -2.86700 Det(Omega_mle): 0.0434311
--------------------------------------------------------------------
Results for equation ice cream
================================================================================
coefficient std. error t-stat prob
--------------------------------------------------------------------------------
const -0.016054 0.034105 -0.471 0.638
L1.ice cream -0.287811 0.079633 -3.614 0.000
L1.heater -0.121251 0.073673 -1.646 0.100
L2.ice cream -0.217862 0.087025 -2.503 0.012
L2.heater -0.081992 0.079793 -1.028 0.304
L3.ice cream -0.122169 0.090772 -1.346 0.178
L3.heater -0.100743 0.080730 -1.248 0.212
L4.ice cream -0.167505 0.089113 -1.880 0.060
L4.heater -0.130541 0.082232 -1.587 0.112
L5.ice cream -0.206725 0.090337 -2.288 0.022
L5.heater -0.168606 0.084980 -1.984 0.047
L6.ice cream -0.138873 0.092630 -1.499 0.134
L6.heater -0.115771 0.089911 -1.288 0.198
L7.ice cream -0.180695 0.092245 -1.959 0.050
L7.heater -0.027255 0.094850 -0.287 0.774
L8.ice cream -0.111166 0.092679 -1.199 0.230
L8.heater 0.041803 0.094740 0.441 0.659
L9.ice cream -0.043835 0.091389 -0.480 0.631
L9.heater 0.012616 0.094705 0.133 0.894
L10.ice cream -0.153345 0.089841 -1.707 0.088
L10.heater 0.059215 0.094546 0.626 0.531
L11.ice cream -0.004417 0.089771 -0.049 0.961
L11.heater 0.042153 0.093799 0.449 0.653
L12.ice cream -0.126643 0.090094 -1.406 0.160
L12.heater -0.021794 0.090097 -0.242 0.809
L13.ice cream -0.081957 0.087069 -0.941 0.347
L13.heater -0.018799 0.079199 -0.237 0.812
================================================================================
Results for equation heater
================================================================================
coefficient std. error t-stat prob
--------------------------------------------------------------------------------
const 0.005855 0.036062 0.162 0.871
L1.ice cream -0.033113 0.084202 -0.393 0.694
L1.heater -0.405367 0.077900 -5.204 0.000
L2.ice cream -0.169804 0.092018 -1.845 0.065
L2.heater -0.193569 0.084371 -2.294 0.022
L3.ice cream -0.048999 0.095980 -0.511 0.610
L3.heater -0.016958 0.085362 -0.199 0.843
L4.ice cream -0.007633 0.094226 -0.081 0.935
L4.heater 0.009474 0.086950 0.109 0.913
L5.ice cream -0.020253 0.095520 -0.212 0.832
L5.heater -0.050607 0.089856 -0.563 0.573
L6.ice cream 0.040645 0.097944 0.415 0.678
L6.heater -0.006504 0.095070 -0.068 0.945
L7.ice cream -0.053440 0.097538 -0.548 0.584
L7.heater -0.053795 0.100292 -0.536 0.592
L8.ice cream 0.074170 0.097997 0.757 0.449
L8.heater -0.059001 0.100176 -0.589 0.556
L9.ice cream -0.004720 0.096633 -0.049 0.961
L9.heater -0.000168 0.100139 -0.002 0.999
L10.ice cream -0.007920 0.094996 -0.083 0.934
L10.heater 0.040322 0.099970 0.403 0.687
L11.ice cream -0.076564 0.094922 -0.807 0.420
L11.heater 0.022568 0.099181 0.228 0.820
L12.ice cream -0.111959 0.095263 -1.175 0.240
L12.heater 0.082608 0.095266 0.867 0.386
L13.ice cream 0.203451 0.092065 2.210 0.027
L13.heater -0.155390 0.083744 -1.856 0.064
================================================================================
Correlation matrix of residuals
ice cream heater
ice cream 1.000000 0.064855
heater 0.064855 1.000000
So our final model is:#
\[
\hat{h}_t = - 0.41h_{t-1} - 0.19h_{t-2} + 0.2i_{t-13}
\]

